ALGUMAS IMAGENS PARA IMPRIMIR E USAR COMO ATIVIDADE EM SALA DE AULA

Regra de Sinais: como é que isto funciona na prática?

Regra de Sinais: como é que isto funciona na prática? 
Adição/Subtração
→ menos com menos: soma e conserva o sinal;
→ mais com mais: soma e conserva o sinal;
→ menos com mais: subtrai e conserva o sinal do "maior".

Multiplicação/Divisão
→ menos com menos: dá mais;
→ mais com mais: dá mais;
→ mais com menos: dá menos.

Mas por que é assim? Como funciona isto na prática?
Vamos descobrir. Vejamos a seguinte situação:

Janaína é dona de um bolicho (denominação dada a um pequeno comércio, onde são vendidos geralmente produtos de alimentação). Ela abastece as suas prateleiras na noite. Na peça que serve para colocar em estoque as suas mercadorias, ela tem 45 kg de arroz e, na prateleira do bolicho, tem apenas 5 kg.

(+5) + (+45) = 5 + 45 = +50 kg = 50 kg 
(mais com mais: soma e conserva o sinal)

Portanto, Janaína tem agora 50 kg de arroz para vender. No dia seguinte, vendeu 35 kg. Sobraram na prateleira 15 kg.
(+50) + (-35) = 50 - 35 = +15 kg = 15 kg 
(mais com menos: subtrai e conserva o sinal do "maior")

Mas, Janaína tinha se comprometido entregar 20 kg para dona Chiquita, que era responsável pela merenda da escola. Dona Chiquita iria fazer um risoto para comemorar o dia do professor. Logo, vão faltar:
(+15) + (-20) = 15 - 20 = -5 kg 
(mais com menos: subtrai e conserva o sinal do "maior")

Janaína também tinha que entregar 10 kg de arroz para dona Genoveva, simpática velhinha vizinha do seu bolicho. Portanto, vai faltar no total:
(-5) + (-10) = -5 - 10 = -15 kg 
(menos com menos: soma e conserva o sinal)

Mas isto não preocupava Janaína, pois o caminhão que fornecia arroz lhe entregaria 50 kg. Logo, ela teria disponível:
(-15) + (+50) = -15 + 50 = +35 kg = 35 kg 
(menos com mais: subtrai e conserva o sinal do "maior")
Logo, Janaína ainda teria 35 kg de arroz na prateleira.

Vamos ver uma outra situação:
Janaína resolve lavar roupa num tanque, na qual uma torneira o enche, colocando a cada minuto, 4 litros de água, ou seja, +4 l/min.

Passados 10 minutos, temos 40 litros de água a mais no tanque:
(+10 ).(+4) = +40 litros = 40 litros 
(mais com mais: dá mais)
No entanto, 2 minutos antes, tinha 8 litros a menos:
(-2).(+4) = -8 litros 
(menos com mais: dá menos)

Janaína enche o tanque, mas verifica que o tanque tem um furo por onde vaza 2 litros de água por minuto, ou seja, -2 l/min.

Em 4 minutos, o tanque terá 8 litros a menos de água:
(+4).(-2) = -8 litros
(mais com menos: dá menos)
No entanto, 3 minutos antes havia 6 litros a mais de água:
(-3).(-2) = +6 litros = 6 litros
(menos com menos: dá mais)

REGRA DE SINAIS

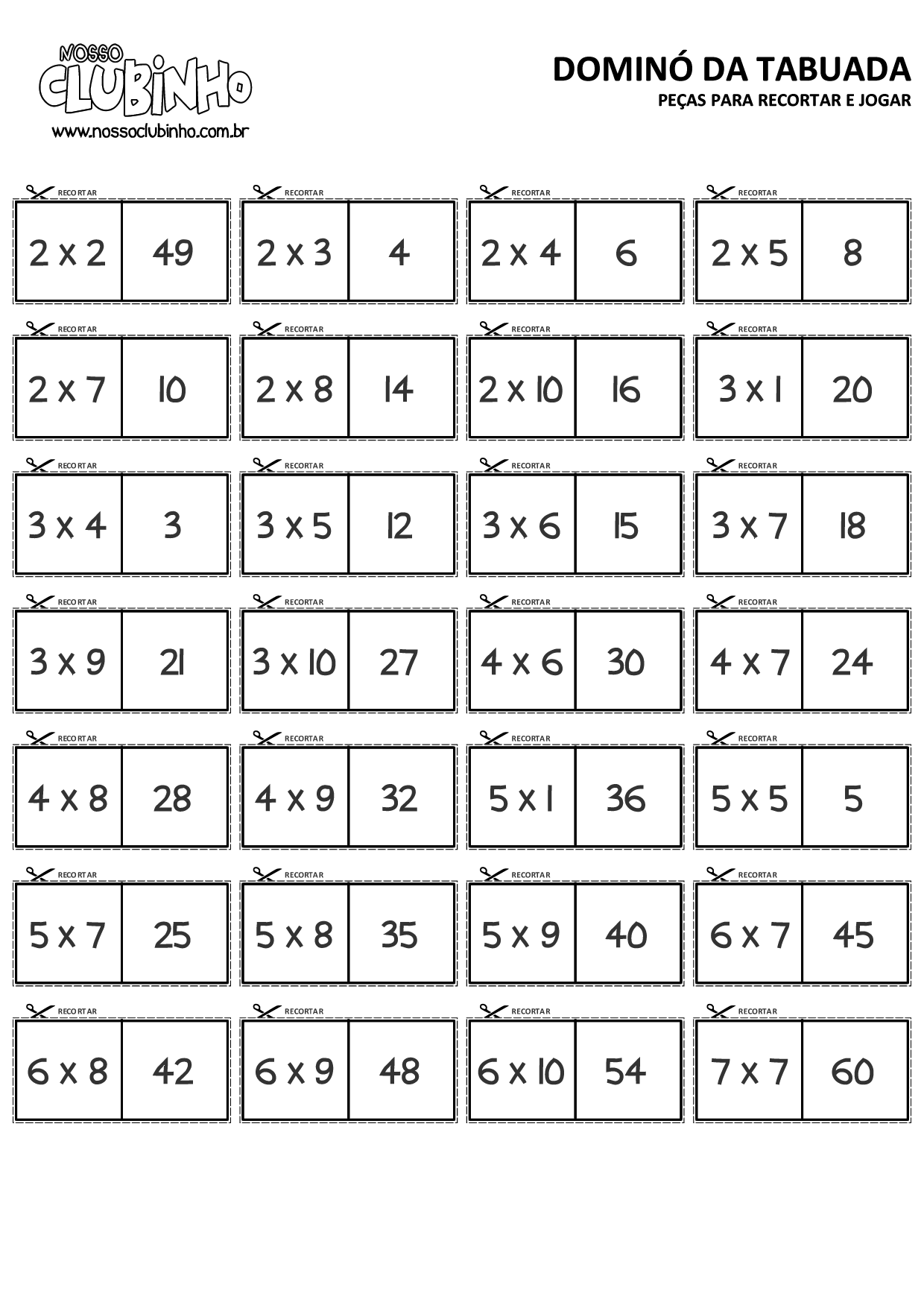
DOMINÓ DA TABUADA

DOMINÓ DA TABUADA

COMO JOGAR:

1. Divida as peças igualmente entre os participantes.
2. Decida quem jogará a primeira peça (pode ser através do par ou impar, uni-duni-tê e etc…)
3. O primeiro jogador a direita, coloca uma peça que resolva a tabuada da peça colocada pelo primeiro jogador. E assim vai indo sucessivamente.
4. Ganha o primeiro a colocar todas as peças na mesa.

VÍDEO JOGO DE DOMINÓ MATEMÁTICO DE ADIÇÃO E SUBTRAÇÃO

JOGO DE DOMINÓ MATEMÁTICO DE ADIÇÃO E SUBTRAÇÃO

 Jogo de dominó da adição e subtração:

REGRAS:

1. Podem participar de 2 a 4 jogadores.
2. Embaralhar as peças com os números voltados para baixo.
3. Cada participante pega uma peça de cada vez no monte, até completar 5 peças. As sobras permanecem no monte.
4. Um participante sorteado (ou com número maior) começa o jogo, revelando uma peça.
5. Cada jogador, um a um no sentido horário, calcula o resultado e junta uma peça no resultado.
6. Quem não tiver a peça, pega sucessivamente do monte até encontrar a peça procurada; se não houver mais peças no monte, passa a vez ao jogador seguinte.
7. Será o vencedor quem ficar sem as peças do jogo em primeiro lugar.

Este jogo pode ser adaptado para multiplicação, divisão e outras operações (há versões com potenciação e raiz quadrada).

TANGRAM

Tangram é um jogo muito utilizado pelos professores de matemática para apresentar aos alunos da educação infantil e do ensino fundamental (até o 6º ano) formas geométricas, trabalhar a lógica e a criatividade, retas, seguimentos de retas, pontos e vértices.

Um pouco de história

Quando surgiu, de onde veio, quem inventou, são dúvidas que nunca foram esclarecidas sobre esse jogo. Existem inúmeras lendas sobre a história do Tangram. Dentre elas a mais comentada é que: um monge chinês deu uma tarefa a seu discípulo, pediu que ele fosse percorrer o mundo em busca de ver e relatar todas as belezas do mundo, assim deu para ele um quadrado de porcelana e vários outros objetos, para que pudesse registrar o que encontrasse. Muito descuidado deixou a porcelana cair, essa se dividiu em 7 pedaços em forma de quadrado, paralelogramo e triângulo. Com essas peças ele notou que poderia construir todas as maravilhas do mundo.

Construção

Quando o professor propuser aos seus alunos o trabalho com Tangram é importante que deixe que eles o construam. O Tangram pode ser construído com EVA ou com papel cartaz, então é preciso que o professor peça que os alunos levem para a próxima aula:

Papel cartaz ou EVA.
Régua
Lápis preto
Borracha

Agora, veja passo a passo como funciona a construção do Tangram.

1º passo: Recorte o EVA ou o papel cartaz em forma de um quadrado:

2º Passo: Trace um segmento de reta que vai do vértice b ao vértice h, dividindo o quadrado em dois triângulos iguais.

3º Passo: Para encontrar o ponto médio do segmento de reta BH, pegue o vértice A e dobre até o segmento BH o ponto de encontro do vértice A e do segmento BH será o ponto médio de BH.

 

Agora trace um segmento de reta que vai do vértice A ao ponto D, formando três triângulos.

4º passo: Dobre o vértice J até o ponto D assim formando dois pontos, um no segmento BJ e outro no segmento HJ.

Agora trace um segmento de reta do ponto E ao ponto I.

5º Passo: Trace uma reta perpendicular do ponto D ao segmento EI.

6º Passo: Trace dois segmentos de reta paralelos ao segmento DG e outro ao lado AH.

Assim, dizemos que um Tangram possui dois triângulos grandes, três triângulos menores, um paralelogramo e um quadrado. Veja essas figuras destacadas:



Recorte todas essas figuras geométricas e terá as sete peças do Tangram.